POLYMÈRES - Théorie sur les polymères

POLYMÈRES - Théorie sur les polymères

Nous nous limiterons ici à l’essentiel des théories actuelles sur les polymères. Nous ne traiterons pas des problèmes de préparation des polymères et des techniques d’études classiques, nous n’étudierons pas non plus les nombreuses applications des polymères qui se retrouveront dans les articles correspondants (cf. ÉLAS- TOMÈRES, PLASTIQUES, RHÉOLOGIE, POLYMÈRES – Polymères thermostables, Polymères conducteurs, etc.).

Nous définirons comme polymères des macromolécules synthétiques formées par la répétition linéaire d’un même motif.

L’exemple le plus simple de polymère est le polyéthylène de formule CH³ 漣(CH²)ⁿ 漣CH³, où n est un nombre qui dépend des conditions de préparation et peut atteindre plusieurs centaines de milliers. Il existe de nombreux autres polymères d’origine synthétique de formule B 漣(A)ⁿ 漣C, où A est appelé le motif monomère. A côté des polymères formés par un seul type d’unité chimique, on produit aussi des copolymères, caractérisés par la présence dans une même chaîne de plusieurs types d’unités répétitives. Ces copolymères sont dits soit statistiques lorsque les positions de A et de B sur la chaîne sont gouvernées par les lois du hasard, par exemple AA 漣B 漣AAA 漣BB 漣A 漣B..., soit alternés lorsqu’ils ont la forme (A 漣B 漣A 漣B)ⁿ , soit encore séquencés si, par exemple, on a une séquence de A suivie d’une séquence de B: AAA 漣BBB.

Il peut arriver que, lors de la préparation de polymères, des accidents introduisent des ramifications dans la chaîne conduisant à des structures du type:

que l’on nomme ramifiées. De plus, on peut préparer des polymères greffés; par exemple, on fait réagir sur une chaîne déjà formée d’autres chaînes portant une extrémité réactive, ou bien on part d’un copolymère statistique A 漣B dans lequel le groupe B sert d’initiateur à la polymérisation d’un groupe C, ce qui conduit à des structures de la forme:

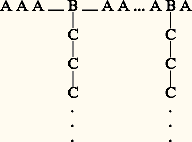Ces structures, surtout si les propriétés des chaînes A et C sont très contrastées, présentent des propriétés très intéressantes, aussi bien du point de vue théorique que de celui des applications. Ce type de polymères peut en particulier former des phases mésomorphes qui ne sont pas sans analogie avec le système savon-eau.

1. Masse moléculaire et indice de polydispersité

Une des difficultés majeures que l’on rencontre lorsque l’on veut se livrer à une étude précise des polymères, que cela soit en solution ou à l’état solide, est liée à la définition de leur masse moléculaire. En effet, de nombreuses propriétés dépendent de cette dernière comme, par exemple, la viscosité à l’état fondu, et toute étude systématique nécessite une connaissance précise du degré de polymérisation, c’est-à-dire du nombre d’éléments monomères dont est constituée la chaîne. Or, la plupart des méthodes de synthèse, et particulièrement les méthodes industrielles, conduisent à des mélanges de chaînes de différentes longueurs. Au lieu de définir le degré de polymérisation N ou la masse moléculaire M de l’échantillon, les méthodes classiques de mesure fournissent des valeurs moyennes. Les plus utilisées sont la masse en nombre Mⁿ et la masse en poids M^w . Appelons nⁱ le nombre de molécules ayant la masse molaire Mⁱ et cⁱ la quantité de matière de même masse Mⁱ (cⁱ = nⁱ Mⁱ ), on définira Mⁿ et M^w par les relations:

Mⁿ est toujours inférieur à M^w et en sera d’autant plus rapproché que la distribution des masses sera plus étroite.

On définira l’indice de polydispersité j comme le rapport M^w /Mⁿ . Des échantillons de polyéthylène préparés par catalyseur Ziegler ont des indices qui peuvent atteindre 8, tandis que, dans les meilleurs cas, des polystyrènes préparés par polymérisation anionique ont des polydispersités inférieures à 1,01 et peuvent être considérés dans beaucoup d’applications comme homogènes.

Caractérisation de la distribution en masse

Il est impossible d’obtenir cet indice par mesure de la valeur absolue des masses, car, malgré les progrès techniques, on ne peut calculer Mⁿ et M^w qu’avec une erreur de quelques pour-cent. Une technique de chromatographie, datant des années 1960, a permis une détermination précise des masses moléculaires et de la polymolécularité. Elle a, de ce fait, augmenté considérablement la précision et apporté un renouveau dans les déterminations expérimentales.

Le principe de cette technique est simple. On part d’une colonne remplie de petites billes d’un diamètre de l’ordre de 10 猪m, formée à partir d’une matière extrêmement poreuse et dont le diamètre des pores dépend de la taille des molécules à étudier. Un solvant circule à vitesse constante dans cette colonne, et on mesure le temps qu’il lui faut pour traverser la colonne. On injecte ensuite au sommet de la colonne, dans le solvant qui circule, une quantité minime de polymère. On constate alors qu’elle sort de la colonne d’autant plus vite que sa taille est plus grande. On peut ainsi, pour une famille de polymères linéaires, établir une courbe liant le temps de rétention à la masse moléculaire, ce qui conduit à une courbe d’étalonnage (fig. 1 a). L’explication qualitative du phénomène est simple: une molécule de taille importante ne peut circuler que dans les pores les plus gros ou dans le volume interstitiel. Elle se déplacera donc plus vite, ne pouvant passer par les petits pores par lesquels passe le solvant. De ce fait, le temps de rétention qui caractérise cette molécule sera plus faible que celui du solvant. Le détecteur en sortie de colonne peut être, soit un réfractomètre qui mesure la concentration par variation de l’indice de réfraction de la solution, soit un spectrophotomètre qui mesure la concentration par l’intensité de l’absorption dans une bande spécifique du polymère.

Si maintenant on injecte un polymère de masse moléculaire bien définie ou au contraire ayant une large distribution de poids moléculaires, on obtiendra des diagrammes tels ceux représentés sur les figures 1 b et 1 c.

Une analyse quantitative d’une telle courbe, en partant de la courbe d’étalonnage et après diverses corrections, permet de caractériser la polymolécularité du système et l’indice i précédemment défini. Cette méthode s’applique à pratiquement tous les problèmes linéaires pour lesquels on a pu trouver un solvant, que ce soit à température ordinaire ou bien à température élevée, comme pour le polyéthylène (150 ⁰C dans le trichlorobenzène).

On conçoit que cette technique, beaucoup plus rapide que l’ultracentrifugation, puisque dans les appareils modernes on peut obtenir un chromatogramme rapidement, ait considérablement amélioré nos connaissances sur les polymères.

Dimensions moléculaires

Depuis les années 1960, l’utilisation de la technique de diffusion des neutrons aux petits angles a, elle aussi, marqué une étape dans le développement de nos connaissances sur les polymères.

On sait qu’un faisceau de neutrons monocinétiques peut être assimilable à une onde sinusoïdale de longueur d’onde = h /m v, où h est la constante de Planck et m la masse des particules ayant une vitesse v. À l’institut von Laue-Langevin à Grenoble, on dispose d’une source brillante de neutrons froids (neutrons ralentis par passage à travers de l’hydrogène liquide) qui ont des longueurs d’ondes de 1 à 2 nanomètres (10 size=1^漣9 m), ce qui est le rayonnement idéal pour étudier des systèmes polymériques dont les dimensions sont de cet ordre de grandeur. Enfin, la diffusion des neutrons par la matière est le fait du noyau et non du nuage d’électrons qui l’entoure. La longueur de diffusion cohérente d’un noyau (paramètre qui exprime l’intensité diffusée par ce dernier) dépend essentiellement de sa structure isotopique; ainsi, le deutérium a une longueur de diffusion cohérente de 0,667 憐 10 size=1^漣12 cm, alors que l’hydrogène, qui lui est chimiquement très semblable, a pour longueur de diffusion cohérente 0,374 憐 10 size=1^漣12 cm. On constate donc que, comme les phénomènes de diffusion dépendent du carré de la longueur de diffusion, il y a presque un rapport de 30 entre l’intensité diffusée par une substance deutérée par rapport à celle que diffuse une substance hydrogénée.

L’intensité diffusée aux petits angles par un système dépend du module du vecteur de 4 神

diffusion q , q = sin 見, où 見 est l’angleentre le faisceau incident et le faisceau diffusé. Dans les installations de diffusion des neutrons modernes, on dispose d’un détecteur bidimensionnel, c’est-à-dire en fait d’un grand nombre de détecteurs placés à différentes valeurs de l’angle 見, ce qui permet en une expérience d’avoir les valeurs de I(q ) où I est l’intensité diffusée dans un domaine relativement étendu de q , c’est-à-dire de 見.

Rappelons que l’étude de I(q ), pour une solution diluée de molécules dans un solvant quelconque, permet d’obtenir le facteur de forme P(q ) de la molécule: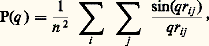

si l’on suppose la molécule formée de n centres diffusants identiques situés à la distance r^ij et si l’on étend la double somme à tous les n ² couples de points i et j .

Si l’on développe P(q ) en fonction de q , on obtient l’expression de Guinier:

où 漣R² est le carré moyen du rayon de giration de la molécule autour de son centre de masse. D’une façon plus générale, I(q ) donne toujours des informations sur la structure des particules diffusantes. Lorsqu’on travaille en milieu plus concentré ou encore en phase condensée, l’interprétation de I(q ) est plus difficile, car cette grandeur dépend des positions relatives de toutes les paires d’éléments diffusants, qu’ils appartiennent ou non à la même macromolécule. Le grand avantage des neutrons est que, en immergeant quelques molécules marquées au deutérium dans un système formé de molécules identiques, au marquage près, on a une solution diluée et l’on atteint ainsi la conformation de la macromolécule. Nous reverrons plus tard quelques applications de cette technique aux problèmes de statistique des chaînes.

2. Configuration des chaînes isolées et en solution semi-diluée

Les conformations d’une chaîne isolée

Du fait des possibilités de rotation autour des liaisons covalentes de son squelette, une chaîne macromoléculaire peut prendre un nombre considérable de configurations. Cela entraîne l’utilisation de méthodes statistiques pour caractériser son encombrement moyen dans l’espace. La quantité la plus utilisée est le carré moyen de la distance entre ses extrémités 漣L². On peut montrer que, quelle que soit la rigidité de la chaîne, si elle est assez longue et si on néglige son volume propre (elle peut passer plusieurs fois par le même point de l’espace), 漣L² devient proportionnel à la masse molaire M et on écrira 漣L² = b ²N = k M, N étant le nombre d’éléments statistiques que l’on peut prendre égal au nombre d’unités monomères et b la longueur du chaînon équivalent.

Ainsi, une chaîne dont la longueur étirée est b N se place en moyenne dans une sphère de diamètre b 連N. De plus, dans le cadre de cette hypothèse, le rayon de giration est égal à 漣L²/6. Si l’on admet que, en moyenne, la chaîne se trouve dans un volume proportionnel à (face=F0019 漣L²)^3/2 ou (face=F0019 漣R²)^3/2, on voit que dans ce volume la densité en segment ou la concentration décroît comme N size=1^漣1/2. Plus la chaîne est longue, plus elle occupe un domaine important dans la solution.

Enfin, la loi de probabilité gouvernant les distances entre deux chaînons est une loi de Gauss.

En fait, l’hypothèse selon laquelle la chaîne n’a pas de volume propre est très restrictive. Elle est approximativement justifiée dans ce que P. J. Flory a appelé un solvant 粒. Lorsqu’on diminue la qualité d’un solvant, généralement par abaissement de la température, il existe, un peu au-dessus du point de précipitation, une température à laquelle les répulsions entre éléments de la chaîne sont exactement compensées par les attractions liées au faible pouvoir solvant. Tout se passe comme si les segments ne se «voyaient» pas, et on est ramené au problème de la chaîne sans dimensions.

On a pu vérifier expérimentalement ces considérations et montrer, par diffusion de la lumière et des neutrons, que, dans un large domaine de masses molaires, le rapport 漣R²/M était constant. De même, l’intensité diffusée par une chaîne, mesurée soit par diffusion de la lumière soit par diffusion des neutrons aux petits angles, obéit bien à l’équation: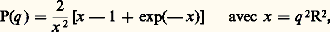

équation caractéristique de la chaîne de Gauss.

Le problème devient beaucoup plus complexe quand on ne peut plus négliger le volume propre de la chaîne ainsi que les interactions répulsives qui, dans un bon solvant, agissent entre unités monomères.

Ce problème a pris le nom de problème du «volume exclu» et a suscité de nombreux travaux pendant une trentaine d’années. La première solution en a été donnée par P. J. Flory, qui a montré que l’énergie libre d’une macromolécule en solution pouvait être séparée en deux termes: un terme élastique qui s’oppose à la dilatation de la molécule et un terme de gonflement qui tend à diminuer la concentration à l’intérieur de la macromolécule, donc à augmenter ses dimensions. En minimisant cette énergie libre, Flory obtient pour les grandes masses et quelle que soit la grandeur de l’effet de volume:

Cette théorie, bien que peu satisfaisante, puisqu’il s’agit d’une théorie de champ moyen qui ignore complètement les fluctuations de concentration à l’intérieur de la chaîne, a fait l’objet de nombreuses vérifications expérimentales.

L’indice fractionnaire 益 rappelle d’une certaine façon les indices critiques anormaux mis en évidence dans de nombreux changements de phase au voisinage du point critique; cela a conduit les théoriciens à se demander s’il n’y avait pas une analogie entre les phénomènes critiques, d’une part, et la statistique des chaînes avec volume exclu, d’autre part.

C’est P. G. de Gennes qui, en 1974, a montré que, formellement parlant, les méthodes utilisées pour étudier la transition magnétique au voisinage du point de Curie s’appliquaient à la statistique d’une chaîne avec volume exclu si l’on donnait au paramètre d’ordre la dimensionalité zéro et si l’on supposait l’absence de champ magnétique. Cette analogie, qui est surtout intéressante du point de vue conceptuel, a incité de nombreux physiciens théoriciens à étudier les macromolécules et, de ce fait, a permis des développements considérables de cette discipline durant les dernières années.

Notons enfin que, alors qu’en solvant 粒 la loi de probabilité est gaussienne, c’est-à-dire que la densité de probabilité pour que les extrémités de la chaîne soient à une distance r est de la forme: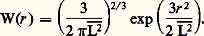

(courbe (a) de la figure 2), les théories et les modélisations sur ordinateur prévoient une allure du type de la courbe (b) de la figure 2.

On voit que la probabilité pour que les extrémités des deux chaînes soient confondues W(0) est maximale dans le cas gaussien, alors qu’elle est nulle pour une chaîne avec volume exclu. On peut expliquer cela qualitativement en disant que le squelette de la chaîne forme une barrière difficile à traverser. C’est peut-être cet effet qui explique les difficultés insurmontables rencontrées par les théories de perturbation pour tenir compte de l’effet de volume pour des chaînes longues.

Solutions semi-diluées

Dans une solution très diluée, le volume disponible pour une molécule est nettement plus élevé que son volume propre, qui est de l’ordre de (face=F0019 漣R²)^3/2; les molécules sont donc en moyenne éloignées et ne se rencontrent que rarement. Si on augmente la concentration, il arrive un moment où les molécules occupent un volume plus grand que le volume de la solution, si elles ne s’interpénètrent pas. La concentration limite entre le domaine des molécules indépendantes et des molécules enchevêtrées est appelée c . Cette concentration est la même à l’intérieur d’une molécule et dans la solution; elle dépend de N suivant la loi:

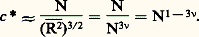Pour 益 = 0,6, elle diminue quand la masse augmente. Ainsi, à titre d’exemple, on obtient une valeur de c de l’ordre de 1 g par 100 ml pour une masse molaire de l’ordre de 300 000. Il existe donc un domaine de concentration caractéristique des solutions de polymère. Si la concentration c est supérieure à c , les molécules perdent leur individualité et s’enchevêtrent en un réseau qui est cependant suffisamment lâche pour que l’on puisse négliger les contacts entre trois segments différents.

En 1974, J. des Cloizeaux a pu montrer, en poursuivant l’idée de P. G. de Gennes, que l’analogie magnétique, en présence cette fois d’un champ magnétique, permettrait d’écrire une équation d’état universelle, correcte dans le domaine des solutions semi-diluées. Cette équation montre, par exemple, que la pression osmotique pour une solution semi-diluée est proportionnelle à c ^9/4 si l’on admet 益 = 0,6, alors qu’une théorie élémentaire, négligeant les fluctuations, donnerait la pression osmotique proportionnelle à c ². Comme c est plus petit que 1, la pression osmotique est plus faible, les segments ont moins de chance de se rencontrer qu’on aurait pu l’estimer.

Quand de très longues chaînes sont en solution, à une concentration supérieure à c , la notion de longueur des chaînes disparaît. Ce qui compte, c’est la taille de la maille du réseau, c’est-à-dire la distance moyenne entre deux points de croisement. Pour un raisonnement simple du type «loi d’échelle» et prenant pour base la théorie de J. des Cloizeaux, on montre que cette distance moyenne que nous appellerons 﨡 dépend de la concentration par une loi de la forme 﨡 年 bc size=1^漣3/4. 﨡 diminue donc quand la concentration augmente; elle est de l’ordre de grandeur de l’élément statistique de la chaîne, b , quand on arrive au polymère amorphe en l’absence de solvant.

Cette distance moyenne est couramment appelée longueur d’écran; elle a été d’abord introduite par S. Edwards, avec des lois de dépendance en c légèrement différentes qui, en fait, correspondent non pas à un bon solvant, comme la théorie de J. des Cloizeaux, mais à un solvant voisin du point 粒.

Pour donner une image simple de la solution semi-diluée, de Gennes a introduit le modèle de ce qu’il appelle le «blob» et que nous allons brièvement décrire. Si on se déplace le long de la chaîne, en partant d’un point de contact avec une autre chaîne et après avoir parcouru une distance dont le carré moyen est de l’ordre de 﨡², on rencontre un second point de contact qui forme écran entre la partie de la chaîne que l’on vient de parcourir et la partie suivante. Il n’y a plus d’effet de volume entre ces deux portions de chaînes, car leurs interactions sont «écrantées» par la chaîne étrangère. Appelons 﨡² le carré moyen de la longueur d’un blob qui comprend g chaînons. Puisqu’il y a effet de volume à l’intérieur d’un blob, 﨡² = b ²g ². Dans la chaîne, il y a N/g blobs et, comme la chaîne de blobs est gaussienne, le carré moyen de la distance entre ses extrémités sera:

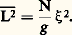Les lois d’échelles permettent de calculer comment ces grandeurs varient avec la concentration de la solution. Ainsi, le rayon de giration est proportionnel à c size=1^漣1/4 et la concentration à l’intérieur d’un blob est identique à la concentration globale de la solution. Tout se passe donc comme si on avait de la matière condensée formée de blobs; il est donc possible d’extrapoler aux solutions semi-diluées les propriétés établies pour les chaînes macromoléculaires à l’état condensé en remplaçant le chaînon statistique par le blob.

Toutes ces considérations ont pu être vérifiées, par l’étude de la diffusion des neutrons aux petits angles, sur des solutions formées de mélange de polystyrène deutéré et hydrogène de même masse en solution dans le sulfure de carbone. En effet, comme le sulfure de carbone et le polystyrène hydrogène ont pratiquement la même longueur de diffusion cohérente, ce sera le polystyrène marqué qui diffusera. Si ce dernier est en solution suffisamment diluée pour qu’il soit possible de négliger les interférences intermoléculaires, l’intensité I(q ) pourra être comparée aux modèles, et on pourra mesurer les lois de variation de 漣L² ou 漣R² avec la concentration et la masse ainsi que la variation de 﨡². Les vérifications qui ont été effectuées depuis les années 1970 se sont avérées excellentes et donnent une base expérimentale solide à ces théories.

Les polymères à l’état condensé

Les polymères amorphes

Un certain nombre de polymères, du fait de l’irrégularité de la position des substituants le long de la chaîne (polymères atactiques), ne peuvent cristalliser.

À haute température, ce sont des liquides viscoélastiques qui, lorsqu’ils sont refroidis au-dessous d’une certaine température, deviennent des verres. Il s’agit simplement d’un blocage des mouvements des chaînes qui, à basse température, ne peuvent passer au-dessus des barrières de potentiel. Cette transition vitreuse est un phénomène tout à fait général, observé aussi bien sur les polymères amorphes que sur la partie amorphe d’un polymère cristallisé.

Le problème de la conformation des chaînes dans un polymère fondu n’a pu être résolu que grâce à la diffusion des neutrons aux petits angles. Conformément aux prévisions de P. J. Flory, les chaînes obéissent à la statistique de Gauss; il n’y a pas d’effet de volume. Pour le vérifier, on a mélangé des chaînes complètement deutérées à des chaînes de même nature et de même masse, mais hydrogénées; le contraste entre ces deux types de molécules permet d’obtenir facilement la fonction P(q ) caractéristique d’une chaîne. On retrouve la formule de Debye, et on obtient les mêmes dimensions moléculaires qu’au point 粒. Les configurations d’une chaîne en solvant 粒 ou dans la masse sont donc pratiquement identiques, bien que les situations soient très différentes. On constate aussi que lorsqu’on diminue la température et que l’on traverse la transition vitreuse pour arriver à l’état vitreux, le diagramme de diffusion n’est pas modifié. Cela a mis fin à une longue controverse. Certains scientifiques prétendaient que, du fait de leur anisotropie, les molécules de polymères devaient, du moins à courte échelle, se ranger parallèlement les unes aux autres. Les neutrons, ainsi que des expériences de diffusion anisotrope de la lumière et des images à fort grossissement prises au microscope électronique, montrent que cela n’est pas le cas.

Pour terminer sur les polymères amorphes, nous rappellerons un autre acquis intéressant. On sait qu’un caoutchouc est formé de chaînes pontées entre elles en certains points, de façon à empêcher les déformations permanentes de l’échantillon (cf. CAOUTCHOUC, ÉLASTOMÈRES). La force de rappel est une force d’origine entropique liée à la déformation des chaînes. On peut, par diffusion des neutrons aux petits angles, étudier un échantillon de caoutchouc étiré dont certaines chaînes sont deutérées. L’intensité I(q ) dépend de l’orientation du faisceau diffusé par rapport à la direction d’étirement. On peut donc mesurer la déformation des chaînes. Des travaux sont en cours, à l’heure actuelle, pour élucider le mécanisme exact de cette déformation.

Polymères cristallisés

Ce que nous venons de dire concerne les polymères amorphes, c’est-à-dire incapables de cristalliser, ou trempés suffisamment rapidement pour en empêcher la cristallisation. Or, beaucoup de polymères réguliers par nature (comme le polyéthylène ou le polyisoprène) ou réguliers par préparations chimiques (isotactiques) peuvent cristalliser plus ou moins complètement. Le problème qui se pose est de savoir comment sont disposées les chaînes dans un polymère cristallisé.

Si l’on part d’une solution diluée d’un polymère cristallisable et que l’on se place à quelques degrés au-dessus du point de précipitation, on voit apparaître des cristaux dont les dimensions latérales sont de l’ordre du micromètre et dont l’épaisseur est de l’ordre de quelques nanomètres (de 4 à 20). Il s’agit donc de plaquettes. Dans ces plaquettes, les chaînes sont disposées, comme cela a pu être mis en évidence par diffraction des électrons, perpendiculairement à la grande surface des plaquettes. Comme les chaînes étirées sont beaucoup plus longues que le petit côté des plaquettes, elles doivent se replier en accordéon. La photo donne une idée de la position des chaînes dans un tel cristal.

Quand on cristallise un polymère en masse, on n’obtient pas de monocristaux, mais toujours un système partiellement cristallisé dont la structure est encore à l’heure actuelle l’objet de nombreuses discussions. Les rayons X montrent que l’on a des lamelles cristallines dont l’épaisseur correspond à peu près à celle des monocristaux. La question qui se pose est de savoir si ces lamelles sont formées de chaînes repliées régulièrement ou si, comme le suggère Flory dans le modèle de micelle, ce sont des segments de chaînes appartenant à des chaînes différentes qui se regroupent pour former les lamelles; il existe sur ce sujet des données expérimentales contradictoires. Ces lamelles se regroupent pour former, à une échelle plus élevée, des sphérolites faciles à mettre en évidence au microscope. Ce type de cristallisation n’est pas une particularité des polymères puisqu’il se retrouve dans d’autres matériaux, particulièrement les minéraux. Lorsqu’on file un polymère cristallin comme le nylon, on étire les chaînes qui recristallisent toujours en lamelles perpendiculaires à la direction d’étirement. On n’obtient ainsi ni le module de Young, ni la résistance à la rupture que l’on peut calculer pour un cristal idéal. Pour atteindre ces valeurs, il faudrait que les chaînes soient toutes complètement étirées et cristallisées parallèlement les unes aux autres. Cela a été réalisé par J. F. Ward et R. S. Porter en étirant lentement un polymère dans une machine, au voisinage de son point de fusion. On arrive alors presque au module théorique, qui est dix fois plus élevé que les modules obtenus par des méthodes classiques. Malheureusement, les fils ainsi formés n’ont aucune résistance latérale; ils se désagrègent en fibrilles, ce qui les rend inutilisables.

Un autre procédé pour obtenir des fibres à haut module a été découvert; il s’applique surtout aux résines connues sous le nom commercial de Kevlar. Ces polymères, qui sont des polyamides aromatiques, ont la propriété de former des phases mésomorphes en solution. Il s’agit de polymères rigides, c’est-à-dire qui ne peuvent pas se replier aussi facilement que le polyéthylène. En solution, au-dessus d’une certaine concentration, la thermodynamique montre que l’on peut avoir une phase intermédiaire dans laquelle les molécules de polymères s’orientent parallèlement les unes aux autres comme dans un cristal nématique. Ce phénomène est très général; il a été observé d’abord sur les polypeptides synthétiques, puis ensuite sur des dérivés cellulosiques. L’intérêt de ces solutions, analogues aux cristaux liquides, réside dans le fait que si, partant d’une telle solution, on procède aux opérations de filage, on obtient une fibre cristalline dans laquelle toutes les molécules sont parallèles; cela permet d’atteindre des modules théoriques. À poids égal, le module de ces fibres est plus élevé que celui de l’acier, ce qui ouvre de nombreux domaines d’applications à cette nouvelle classe de polymères.

3. Mouvements dans les polymères

Dans tout ce qui précède, nous n’avons parlé que des propriétés statiques des chaînes, étudiant leurs configurations à l’équilibre.

Il est évident que, en raison de l’agitation thermique, dès que les chaînes sont à l’état liquide ou en solution, elles ne restent pas figées dans une configuration mais se déforment perpétuellement. De plus, si on soumet le milieu à une contrainte, les chaînes se déplacent en se déformant; ce sont ces mécanismes qui sont responsables des propriétés mécaniques remarquables des polymères, telles qu’elles sont étudiées dans les expériences de viscoélasticité par exemple.

Le problème qui, du point de vue théorique, est le plus simple et qui, ces derniers temps, a été systématiquement étudié grâce aux techniques de la diffusion quasi élastique de la lumière et des neutrons, est celui des mouvements d’une chaîne.

Nous avons admis plus haut que la lumière diffusée avait la même longueur d’onde ou la même fréquence 益⁰ = 諸⁰/2 神 que la lumière incidente. En fait, comme les molécules se déplacent, la lumière diffusée n’a pas forcément la même longueur d’onde et il est possible d’analyser la répartition spectrale de l’intensité diffusée I(q , 諸 漣 諸⁰), c’est-à-dire de mesurer, à q constant, l’intensité diffusée en fonction de 諸 = 2 神益. Si l’on se place à un angle q tel que q R 廉 1, les molécules se comporteront comme des points et I( 諸) dépendra uniquement du mouvement de leur centre de masse. Sa mesure permettra de déterminer ce que l’on appelle le coefficient de diffusion de translation des molécules, qui se définit ainsi: si l’on regarde le mouvement brownien de ce centre de masse, le carré moyen de son déplacement 漣r ² est proportionnel au temps t , et, en écrivant 漣r ² = 6Dt , on définit le coefficient de diffusion D; il est aussi égal à k T/f , où f est le coefficient de frottement visqueux, c’est-à-dire le rapport de la force F appliquée à une molécule à la vitesse moyenne qu’elle rend sous l’action de cette dernière. L’intensité I(q , 諸) prend alors la forme:

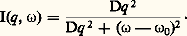C’est l’équation d’une courbe appelée une lorentzienne et dont la largeur à mi-hauteur est ( 諸^1/2 漣 諸⁰)² = Dq ². Cela permet de mesurer D. En portant ( 諸^1/2 漣 諸⁰)² en fonction de q ², on obtient une droite, si le système obéit aux lois classiques du mouvement brownien; sa pente permettra de déterminer D.

Si maintenant on opère en solution diluée, mais à des valeurs de q telles que q R 礪 1, ce que l’on verra sera le mouvement relatif de deux centres diffusants placés sur la même molécule. Il faudra, pour évaluer ces mouvements, tenir compte à la fois de la flexibilité de la chaîne et du frottement hydrodynamique qui s’exerce entre les éléments qui la composent, d’une part, et le milieu dans lequel elle évolue, d’autre part. Ce problème a été résolu en première approximation par P. Rouse, puis par B. Zimm; ils ont montré l’un en négligeant les interactions hydrodynamiques, l’autre en en tenant compte, qu’on pouvait décomposer le mouvement des chaînes en une série de modes analogues aux harmoniques d’une corde vibrante. Ces théories prévoient que la fonction I(q , 諸) n’est plus que lorentzienne et que sa largeur à mi-hauteur se met sous la forme d’une loi de puissance ( 諸^1/2 漣 諸⁰)² 年 qⁿ , avec n = 4 pour le modèle de P. Rouse et 3 pour le modèle de B. Zimm et de P. G. de Gennes. Ces prévisions théoriques ont été soumises au contrôle expérimental par diffusion quasi élastique de la lumière et des neutrons, technique qui permet d’atteindre, vu la différence des longueurs d’onde, des domaines de q très différents. Les résultats confirment de façon relativement satisfaisante la théorie, mais il y a encore un certain nombre de points qui méritent clarification.

Mouvements dans les polymères fondus

Il est tentant, en première approximation, de supposer que, dans un polymère fondu, une molécule se déplace au milieu des autres molécules comme si ces dernières étaient simplement un solvant très visqueux. Cela revient à appliquer la théorie de Rouse et fournit une relation linéaire entre la masse molaire et la viscosité. Effectivement, l’expérience conduit à ce résultat pour des masses peu élevées et lorsqu’on travaille à des vitesses de cisaillement suffisamment faibles pour éviter la déformation des chaînes. Si, cependant, on augmente la masse, la courbe log 兀 en fonction de log M change brutalement de pente, la viscosité 兀 devient proportionnelle à M^x , x étant de l’ordre de 3,3. La masse molaire M^c au niveau de laquelle s’effectue ce changement de comportement est bien définie et dépend du type de polymère considéré. Elle est de 4 000 pour le polyéthylène et atteint 38 000 pour le polystyrène. On explique ce phénomène ainsi: au-dessous de M^c les chaînes sont assez courtes pour se déplacer individuellement, tandis qu’au-dessus de cette masse critique, les chaînes sont enchevêtrées. Dans son mouvement, une chaîne entraîne d’autres chaînes macromoléculaires, ce qui augmente considérablement la viscosité du milieu.

La description de ce phénomène complexe est difficile mais un nouveau mécanisme a été proposé, qui jette un jour nouveau sur tous les problèmes rhéologiques. Il s’agit du mécanisme de «reptation» proposé par S. Edwards et P. G. de Gennes. Si l’on suppose une chaîne déployée dans un plan, ce plan coupe les autres chaînes en une série de points. Un déplacement latéral de grande amplitude est impossible, car il faudrait que la chaîne déplace une autre chaîne. Le mouvement le plus facile qui reste à la chaîne consiste donc à se déplacer dans un sens ou dans un autre le long de sa trajectoire, un peu comme un serpent qui se déplacerait sur un terrain planté d’arbustes, ce qui explique le vocable reptation utilisé pour caractériser ce mouvement. Selon S. Edwards, les obstacles caractérisent un tube dans lequel la molécule a une certaine mobilité. Supposons un système déformé dans la direction générale du tube, si l’on relâche la tension sur les extrémités de la chaîne, un premier mécanisme de relaxation rapide fera revenir la chaîne à une conformation plus probable à l’intérieur du tube, et ensuite, par reptation, elle sortira du tube par les bouts pour en créer un autre. Les calculs relatifs à ce modèle sont relativement aisés puisque, rappelons-le, les polymères fondus obéissent à la statistique de Gauss. Ils ne s’appliquent évidemment qu’au-dessus de la masse critique M^c , car, au-dessous, comme il n’y a pas d’enchevêtrement, la chaîne est plus courte que deux obstacles consécutifs qui matérialisent le tube et il n’y a plus de tube. Les premiers résultats de ce modèle conduisent à un coefficient de diffusion de translation proportionnel à M² et à une viscosité proportionnelle à M³. La première conclusion relative à la diffusion de translation a été vérifiée en mettant en contact deux échantillons dont l’un contient un polymère marqué au deutérium et en suivant, au cours du temps, la migration des molécules marquées dans le polymère non marqué. Il est évident que, pour que le modèle de reptation soit utilisable, il faut que les molécules du réseau soient assez longues. En fait, il s’applique beaucoup mieux au mouvement d’une longue chaîne emprisonnée dans un réseau, comme cela a été vérifié par J. D. Ferry.

M. Doi et S. Edwards ont tenté, en partant de ce modèle, d’obtenir des équations qui permettent une description quantitative complète du comportement viscoélastique des polymères, c’est-à-dire de calculer les déformations d’un échantillon en fonction des contraintes qui lui sont appliquées.

Le domaine des applications des polymères est très vaste, puisqu’il va de la médecine (encapsulation des médicaments, biomatériaux) à l’électronique (polymères semi-conducteurs, piles photovoltaïques), l’industrie automobile, en passant par la floculation des eaux polluées, l’hydrométallurgie et la récupération assistée du pétrole, pour ne citer que quelques-uns des domaines qui suscitent le plus d’intérêt parmi les chercheurs.

Encyclopédie Universelle. 2012.